【まだ書きかえます。どこをいつ書きかえたかを必ずしも明示しません。】
- 1 -
気候には、陸上と海上、あるいは内陸と沿岸とで、ちがいがあらわれることがある。
「大陸性」と「海洋性」の気候の特徴は、乾湿をさすこともあるが、気温についていうならば、大陸の内陸のほうが沿岸よりも夏と冬との気温の差 (年較差) が大きいのだ。
また、関東平野のうちでは内陸の熊谷では夏の晴れた昼に気温がとても高くなるが、東京湾岸の地点ではそれほど高くならない。内陸のほうが沿岸よりも昼と夜の気温の差 (日較差) が大きいのだ。(ただし、年変化についてみると、わたしが検討できたのは振幅ではなくて位相についてなのだが、熊谷と東京湾岸ぐらいの距離では、ほとんどちがわないようである。)
海陸風は、地上気温の日変化が陸のほうが大きいからおこる。昼には陸に接した空気が海に接した空気よりも温度が高く、したがって軽く (密度が小さく) なり、それが上昇したところの下層に海風がふきこむ。夜には海上のほうが相対的に温度が高いから、海上に上昇流ができ、下層で陸風が海にむかう。
季節風にも、年変化について同様なしくみがはたらいている。ただし熱帯のモンスーンのばあいは、このしくみでできるのはいわゆるプレモンスーン (pre-monsoon) の循環であって、モンスーン本番では雲のなかで水が凝結する際の潜熱の解放が循環のおもな動力源になっている。
- 2 -
このようなことがおこる原因を、「陸は海よりもあたたまりやすくさめやすいから」と説明されることがある。また「海は陸よりも熱容量が大きいから」と説明されることもある。これはよい。しかし、(おそらく同じことを言っているつもりで) 「海は陸よりも比熱が大きいから」と説明されることがある。これはまずい。
熱容量とは、物体の温度を上げるのに必要なエネルギーを、単位温度あたりでしめしたものである。SI単位では、エネルギーの単位はジュール (J)、温度の単位はケルビン (K) だから、熱容量の単位は J/K となる。ただし、ケルビンとセルシウス度(℃) とは、原点はちがうが温度差に関するかぎり同じだから、J/K は J/℃ としても同じことだ。
同じ物質の質量を2倍にすると熱容量も2倍になる。質量あたりの熱容量は物質の性質だ。厳密には温度によってもいくらか変化するが、物質ごとに定数とみなしてよいことがおおい。物理用語で「比-」という接頭語 (英語では specific という形容詞) は「質量あたり」という意味につかうことがおおい。「比熱容量」は質量あたりの熱容量だ。「比熱」ということばは (語源がそれだったかは確認していないが) この「比熱容量」の省略表現だといえる。
かつて、「熱量」の単位としてカロリー (cal) がつかわれた。これは、水 1 g を温度 1℃ だけ上げるのに必要な熱量とされた。それから、熱力学第1法則が確立し、熱と仕事は同じ種類の量であることがわかった。エネルギーの単位は、仕事の単位として、メートル (m)、キログラム (kg)、秒 (s) からくみたてられたジュール (J) がつかわれるようになった。1カロリーは約 4.2 ジュールである。いいかえると、水の比熱容量は 4.2 × 103 J / (kg K) なのだ。(kg と g の換算があるので10の3乗がかかっている。なお、ここではわざと有効数字を2けたまでにした。3けためは温度がなん℃の水を1度あげるかによってかわるので、カロリーの精密な定義は複数のものがある。)
岩石の比熱容量は、およそ 1 × 103 J / (kg K) ぐらいだ。土壌の比熱容量は水をどれだけふくむかによってかわってくるが、岩石と水とのあいだにくるだろう。したがって、海を構成する水は陸を構成する物質よりも比熱容量が大きいという文は真ではある。しかし、せいぜい4倍であり、けたちがいに大きいわけではない。さらに、水の密度はよい近似で 1 × 103 kg/m3 だが、岩石の密度はその 2 倍ぐらいだ。比熱容量と密度をかけて体積あたりの熱容量で見れば、海は陸のせいぜい2倍だ。
- 3 -
気候の形成にとっての海陸の熱的性質のちがいをかんがえるときは、地表面 (海面や地面) の単位面積あたりの熱容量 (SI単位は J / (m2 K) ) をくらべるべきなのだ。
かりに、地表面で海と陸にあたえられたエネルギーが、それぞれ一定の厚さの層のうちに均一に分配され、その層より下とのやりとりは無視できるとしよう。そのばあい、層の単位面積あたりの熱容量は、体積あたりの熱容量に層の厚さ (鉛直方向の長さ) をかけたもの、いいかえれば、比熱容量と密度と層の厚さをかけたものとなる。海と陸の熱的性質のちがいをもたらす最大の要因は、層の厚さのちがいなのだ。
岩石は固体だから (しかも光などの電磁波に対して不透明だから)、そのなかの熱伝達のしくみは熱伝導だけだ。土壌はいくらかの水をふくんでいるが、ほぼ固体とみなせる。それに対して海 (や湖など) は流体だから、熱伝導のほかに、質量をもつ物質が動くことによる熱伝達がある。(そのような熱伝達は、熱伝達論では「対流」とよばれる。それには気象学や海洋学でも「対流」とよばれるようなかたちの運動によるものもふくまれるが、もっとこまごました「乱流輸送」とよばれるものもふくまれる。) その結果、日変化や年変化にかかわることができる層の厚さが、海では陸よりもけたちがいに大きいのだ。
ちょっとややこしいことに、日変化と年変化にかかわる層の厚さは同じではない。現実には熱が層のうちで均一に分配されるという仮定がなりたっていないからだ。
とくに熱伝導のばあいは、地表面で変動する熱をあたえられたことによって生じる温度の振動が下にしみこんでいくにしたがって、振動の振幅は指数関数型で小さくなっていく。しみこみかたはあたえる振動の周期 (時間) によってちがい、しみこむ深さのスケールは周期の平方根に比例する。年変化の周期は日変化の周期の約400倍だから、年変化のしみこむ深さは日変化のしみこむ深さの約20倍ということになる。このような層が地表面温度の変化におよぼす効果を、あえて均一な層で近似するとしたときの層の厚さは、振動の振幅が表面での振幅の (1/e) (ただし e は 約 2.7) になる深さをとるのがよいとされる。わたしは、下にあげる例を参考にしながらおおざっぱに、日変化にかかわる層は 5 cm ぐらい、年変化にかかわる層は 1 m ぐらいをとるのがよいと思っている。100年間の気候変化を考えるならば 10 m の層を、1万年間ならば 100 mの層を考えるべきだろう。
水の層のばあいは水が上下に入れかわるしくみがいろいろありうる。温帯の海での年変化についていえば、冬に表面でひやされて密度が大きくなった水が沈むことによる対流で、表面から深さ100 mぐらいまでがだいたい同じ温度になる。夏は表面があたためられて対流がおきにくいので大きな鉛直温度勾配が生じる。しかし冬にだいたい同じ温度になるところまでを海洋表層の「混合層」とみなすことがある。海面水温の年変化のおおまかな見積もりのための近似として、熱が深さ100mの混合層に均一に分配されるとみなすことがある。海面水温の日変化についてどのような厚さの層をとるべきかわたしはよく知らないが、もし熱伝導のばあいから類推して年変化にかかわる層の 1/20 ぐらいと考えてよいとすれば、5 m ぐらいということになる。
- 3 -
わたしの勤務先の大学で、気象の連続観測をして、10分ごとの値を記録している。そのうちに、深さ 5 cm、10 cm、30 cmの地温がふくまれている。こころみに、ある1週間の10分ごとの値をグラフにしてみた。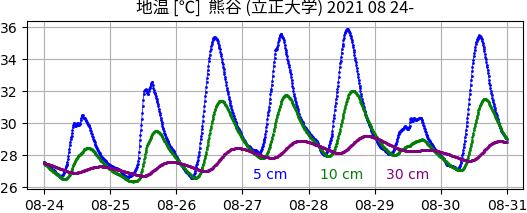
海の水温を複数の深さで日変化がわかる時間分解能で観測しているデータをさがしたら、つぎのウェブサイトがみつかった。
- 水産研究・教育機構 リアルタイム海洋情報収集解析システム https://buoy.nrifs.affrc.go.jp/
わたしはまだ多数の地点・日時のデータを見ていないが、ひとまず、妻良 (めら、静岡県 南伊豆町、水深 約 27m) の深さ 1 m, 5 m, 10 m, 20 m の、上の例と同じ1週間の毎時の値をグラフにしてみた。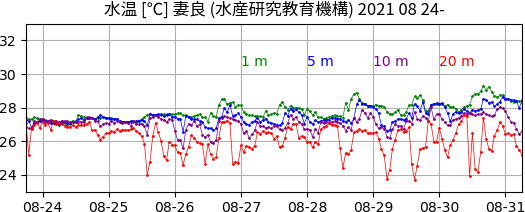
水温の変化には、陸の地温の日変化とその深さによる変化とはちがう特徴がみえている。観測があるうちでいちばん深い 20 m の層の水温の変化が大きいが、それは日変化とはちがうようだ。おそらくこの場所の海底付近の流れによって不規則に変化がおきるのだろう。1 m、5 m、10 m の水温は、図にしめされた期間の3日め以後には午後に高めになる日変化があり、極大の時刻は深くなるほど少しずつ遅くなっているように見える。ただし振幅はあまりかわらず、熱伝導の理論からえられる指数関数型の減衰とはちがうようだ。日変化にかかわる実効的熱容量の形にまとめるのはむずかしい。[この段落 2026-01-11 改訂]
- 4 -
この問題をおおやけに指摘しようと思ったきっかけは、つぎの高校の教科書の記述を見かけたからだった。
- 前田 京剛 ほか 27名, 2023: 『物理基礎』 [2・東書・物基 701]。東京書籍, 288 pp. ISBN 978-4-487-16623-7. [読書メモ]
1990年代ごろの教科書検定では学習指導要領の範囲外のことを書くことがとがめられたが、ちかごろでは「発展」と明示すれば範囲外のことを書いてよくなった。この本は『物理基礎』の教科書のうちでもとくに発展の話題が多い本だ。そして、これは発展ではなく「物理基礎」で学ぶ概念の応用という位置づけのようだが、「熱」の章の「熱容量と比熱容量」の小節に「比熱容量と気候」というコラムがある (143ページ)。
そこでは、東京と「クブチ砂漠」の3日間の気温の時系列グラフが示されていて、日変化の振幅は東京のほうが小さい。それが、比熱容量が、海水では 3.9 J/(g K) であるのに対して砂や岩ではその約 1/5 の 0.8 J/(g K) であるからだ、という説明になっている。
このような話題は高校理科ではふつう地学に分類されるけれども、物理の熱に関する知見の応用例としてしめすのは、気候専門家からみてありがたいことだし、物理の教育の動機をふやすためにも有意義だとおもう。しかし、せっかく本文で「熱容量と比熱容量」を説明しているのに、コラムでは比熱容量だけの話にしてしまったのはうまくない。ここでは温度変化がおよぶ層の厚さのちがいを考慮して面積あたりの熱容量のちがいとして論じてほしかった。