- 0 -
[2020-03-21 の記事]で、オーバーシュート (overshoot) ということばの話をした。そこでものべたように、わたしは、感染症のひろがりについて使われるばあいに、このことばの意味はきちんときまっていないので、ほかに適切な表現があればそちらをつかうべきだ、ぜひこのことばをつかいたいならば、いまの文脈ではどういう意味なのかをよく説明してからにするべきだ、と思っている。
- 1 -
オーバーシュートと表現されていたうちには、「指数関数型の増加」(exponential increase)、「指数関数型の成長」(exponential growth)と表現するのが適当なばあいがあるらしい。[2020-03-21の記事] の最初の(手がきの)図の「(z)」のような状況にあたるだろう。
「指数関数」ときいてもなんのことかわからない人にむけては、「急激な増加」「急激な成長」とするのが、現実的には適切かもしれない。しかし「急激な」では、つたえたいことがぼけてしまう。「急激な」と表現されたとしても、そのもとが「exponential」や「指数関数型」であることを知った人にはもうすこし正確な意味がつたわるように、この用語の説明が用意されているのがよいと思った。
指数関数型の増加は、わたしの本業の(科目名は まちまちだが、内容に即してなづければ) 気候システム論の授業の受講生にぜひわかってもらいたい基礎概念のひとつでもある。そのための教材用ウェブページをすでにつくってあるつもりでいたのだが、それは、黒板または白板に図をかきながら講義するときの補足説明のための簡単なものだった。これからの学年には、遠隔で授業をする必要があるかもしれないから、教材はなるべく読んでわかる形に書いておきたいと思う。ひとまず、このブログ記事で、説明をこころみてみる。ただし、思いつくままに書いていくので、教材ページというよりも、漫談的なブログ記事になってしまうかもしれない。
- 2 -
指数関数は、exp(t) または et とかかれる関数だ。
t は、あとで時間をさすものとしてつかうので、この文字にしておいたが、数学の関数としては、特定の量にむすびついたものではなく、数である。tも、結果として得られる exp(t)の値も、連続量をあらわす数、数学用語でいう「実数」の値をとるとする。
指数関数という名まえがついているのは、aの2乗 (つまり a かける a) が a2 であるのと同様な意味で、et は「 e の t 乗」だといえるからだ。a2での 2 のようなものを「指数」(英語では exponent)という。tの関数である exp(t) = et は、「tが指数の位置にくる関数」なので指数関数とよばれるのだ。
e は定数で、実数値をとり、十進小数の有限けたではかけないが、上位のけただけ数値をしめせば、2.718 ... だ。
代表的な t の値に対する exp(t) の値をあげておく。
- exp(1) = e
- exp(0) = 1
- exp(-1) = 1/e
- 2X [2020-03-26 追加] -
ここで、「exponential」という英語の形容詞に対応する日本語を「指数関数型の」とした。単語の直訳ならば「指数の」「指数的な」でよいところだが、わたしはそうするのをさけている。それには、つぎのような理由がある。
ひとつには、日本語の「指数」には、英語の「exponent」とはちがう意味もあるからだ。たとえば、「物価指数」の「指数」は、英語ならば「index」だ。
もうひとつには、数学の「指数」(exponent) をふくむ関数は指数関数だけではないからだ。たとえば、tp (t の p乗。t が変数、p は定数とする) は、t の関数ということができ、p を指数(exponent)としてふくむけれども、指数関数ではなく、t のベキ[冪] 関数だ。
- 3 -
時間にともなって変化する数量をあつかうとき、指数関数が重要なのは、指数関数がつぎのような単純な微分方程式の解になっているからだ。(ここで、数学としては厳密ではないが、物理などではふつうのように、Xという量があって、時間 t とともに変化するとき、時刻 t での X の値をも、t から X をもとめる関数をも、X(t) とかいてしまうことにする。)
d X(t)/dt = a X(t) (ただし、a は定数とする。) ... (1)
つまり、Xの単位時間あたりの変化量が、X自身の現在の値に比例する、という状況である。
これの解は、つぎのようになる。
X(t) = X(0) exp(a t) ... (2)
(これは、X(0) と exp(a t) との積で、代数の習慣どおり、かけざんの記号が省略されている。「a t」は定数 a と変数 t の積である。)
X(0)は時刻 0 での t の値で、時間変化を考える文脈では定数である。これを「X の初期値」ということがある。この用語については、[2014-02-01の記事]で説明した。
a の値が 1, 0, -1 であるばあいのグラフをかいてみた。ただし、便宜上、X(0) = 1 とした。
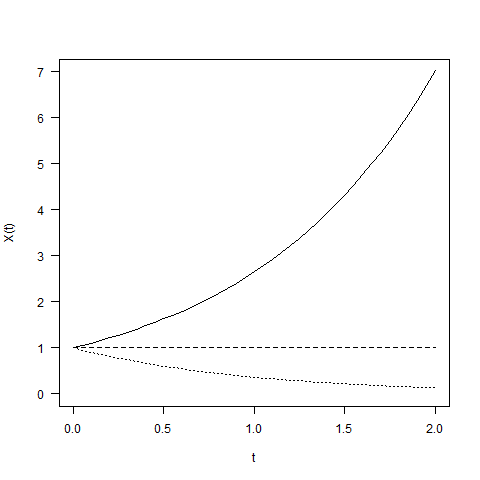
X(0)と a がいろいろな値をとっても有効になるように、この特徴を説明してみる。ただしX(0)が正であることを想定する。(X(0)が負のばあいは、ここからの議論の「X」は -X をさすものとしたうえで、そのばあいに X はどうなるかを考えればよい。)
- a = 0 のばあい(グラフの破線)は、X は時間とともに変化しない (定数である)。
- aが正のばあい(グラフの実線)は、X は時間とともに増加するのだが、その単位時間あたりの増加量 (増加の rate, dX/dt) も時間とともに増加する。グラフでいえば、曲線の傾きが右にいくにしたがって大きくなっていく。
- aが負のばあい(グラフの点線)は、X は時間とともに減少して、0 にちかづいていく。その単位時間あたりの変化量の絶対値も、時間とともに減少する。
- 4 -
現実世界のものごとは複雑だが、そのふるまいが、指数関数で近似できるばあいがある。
指数関数的増加は、爆発的現象に対応することがおおい。現実世界で、指数関数的増加が長期間にわたってつづくことはおこりにくい。それは、現実世界で X の量をふやすしくみには、資源の限界があるので、X の値がおおきくなっていくと、式(1) がそのしくみのよい近似でなくなるからだ。世界全体の経済活動の成長にも限界があることを、わたしは[2019-09-28の記事]などたびたび論じてきた。
指数関数型減少のほうは、現実の変量 Z が、その代表的な値 Z0 のまわりをゆらいでいるとき、X = Z - Z0 としてえられた X についてならば、よくみられる。ただし、それを知るには、Z をよい精度で計測する必要があるだろう。
- 5 -
指数関数型の増加と減少は、計測・制御工学あるいはサイバネティクスでいう「フィードバック」とも関係がある。XがYを変化させ、その影響がXにかえってくる。それがつぎの式のような形をしているとしよう。
Y(t) = p X(t) (pは定数) ... (3a)
d X(t)/dt = q Y(t) (qは定数) ... (3b)
ここで p かける q を a として、X だけの式にすれば、(1)とおなじになる。
- p かける q が正のときが「正のフィードバック」で、X は時間とともに指数関数型で増加する。
- p かける q が負のときが「負のフィードバック」で、X は時間とともに指数関数型で減少する。
(ただし「増加」「減少」という表現は X が正の値をとることを想定している。)
- 6 -
「指数関数型増加 (exponential increase)」とたびたび対比される概念として、「直線型増加 (linear increase)」がある。これは、
X(t) = X(0) + a t (a は定数) ... (4)
のような形の時間変化をさす。(この a は (1)式の a とは関係ない。)
微分方程式でかけば
d X(t) / dt = a (a は定数) ... (5)
のような問題の解だということもできる。
英語の linear の訳語としては、「線形」[せんけい]がつかわれることがおおい。
しかし、この用語はとてもまぎらわしい。幾何学用語としては、「点」が0 [ゼロ]次元、「面」が2次元、「立体」が3次元の図形であるのに対して、1次元の図形を「線」という。そこでは曲線も線なのだ。ところが、関数の話をするときの linear は、そうではなく、一般には曲線であるグラフが、直線になるようなばあい、関数としては「1次関数」になるばあいをさしている。この「1次関数」は、多項式のうちの1次式であらわされるような関数、という意味だ。(同様に「2次関数」「3次関数」...)がある。一般社会でよくつかわれる「一次的」「二次的」とは意味がちがう。
もうひとつまぎらわしいことに、微分方程式の分類としては、(1) のような式も線形の微分方程式であり、フィードバックシステム論では、(3a)(3b)のようなシステムも「線形システム」なのだ。(むしろ、これこそ「線形システム」の典型なのだ。)
わたしは、linear increase の linear に対応する日本語として、「線形」は さけたほうがよいと思う。関数の性質という意味では「一次関数型」がよいと思うのだが、「一次」のまぎらわしさもさけたいので、グラフの形をあらわす「直線型」のほうがよいと思っている。
「指数関数型増加は、直線型増加にくらべて急激だ」といわれることがよくある。これが正しいかどうかは、それぞれの係数 a や、初期値 X(0) しだいだ。もし、初期時刻 t = 0 で、Xの値が同じで、グラフの傾きも同じならば、直線型増加のグラフは、指数関数型増加のグラフの t = 0 での接線にあたる。このような状況にかぎれば、たしかに、指数関数型増加のほうが「急激だ」といえる。
現実の現象は、厳密に指数関数型でも、厳密に直線型でもないことがおおい。それでも、どちらのほうがよい近似になるかを考えることが有意義なことがおおい。
- 7 -
「指数関数型」対「直線型」と、同じでないが同様な対比として、「等比数列型」対「等差数列型」がある。(「数列」のところが「級数」になっていることもある。「数列」と「級数」との意味のちがいもあるのだが、ここではそれに深入りしない。なお、いまの数学ではつかわれていないが、経済学の古典などにのこっている表現として、「等比級数」を「幾何級数」、「等差級数」を「算術級数」ということもある。)
よくつかわれる例に「ねずみ算」がある。変化する量は生物の個体数で、整数だ。時間も、その生物の1世代にあたる時間きざみの整数倍をとる、とびとびの(離散的な)ものとして考える。有性生殖をするネズミをあつかうとちょっとめんどうなので、細胞分裂でふえる単細胞生物を想定しよう。第1世代の個体数が 1 で、1世代ごとに2倍になるとすれば、第n世代の個体数は、2n-1 となる。これが、等比数列の典型的な例だ。
もうひとつよくつかわれる例として、おかねの利子がある。このばあいも、ふつう、時間は、約束によって、1年あるいは1か月などの一定間隔でとびとびのものを考える。金額は、本来はたとえば「円」単位の整数値をとるのかもしれないが、ここでは、たとえばなしなので、実数値をとりうる変数とみなしてしまおう。初期金額 X(0) で、年利 r [注] の「複利」ならば、n 年後の元利合計は、X(0) (1 + r)nとなる。これは等比数列になる。他方、同じ利率でも「単利」ならば、n 年後の元利合計は X(0) (1 + n r) だ。これは等差数列になる。
- [注] ここでは利率 r は単純に「利子 / 元本」の比だとする。たとえば、利率が「3 %」、あるいは、割[わり]・分[ぶ]・厘で「3分」と表現されていたならば、r = 0.03 である。
時間きざみをこまかくした極限では、等比数列は指数関数、等差数列は1次関数(グラフでいえば直線)にちかづく。
- 8 -
放射性核種についてつかわれる (ほかの話題にも応用される) 「半減期」や、いろいろな物理・化学的システムの状態量についてつかわれる「時定数」という概念も、指数関数型の時間変化に関連する。ひとまず、(1)や(2)が現象のよい近似になっているばあいについて、
- 「時定数」は、(1)や(2)での 1/a の絶対値に対応する、
- 「半減期」は、aが負のばあいの、「時定数」の loge(2) 倍 (約 0.7 倍)に対応する、
とのべておく。必要を感じたとき、別の記事にしたい。